『Scratch』で『Sin関数』と『曲線運動』を学ぼう

『Scratch』では、お手軽にプログラミングを体験することができますね。その Scratch の中で、『三角関数である Sin(サイン)』を活用して、『曲線運動をプログラミング』してみましょう!
Table of Contents
この記事でできること
この記事で紹介する Scratch のプログラミングで、動画と同じことができます。
後半に Sin 関数を応用したおまけ動画もありますよ♪
Scratch でプログラミングしてみよう!
本記事で扱う Scratch のバージョンは 3.x系です。Scratch の基本操作は省略します。
以下の公式サイトで直接プログラミングをすることもできますし、サイトから Scratch 本体をダウンロードすれば、インターネット環境がなくても Scratch を扱うことができます!
Scratch の Sin 関数
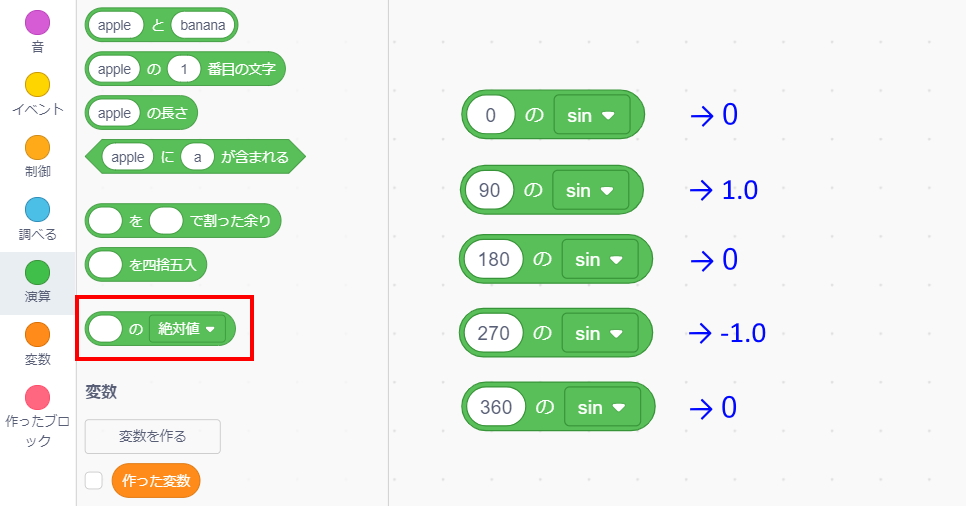
Scratch の『演算』項目にある『○○の絶対値』を『○○の Sin』に変更して使います。任意の数値を渡すと、『-1.0 ~ 1.0 の値』になって返ってきます。
Sin 関数でフワフワ移動する Scratch のネコ
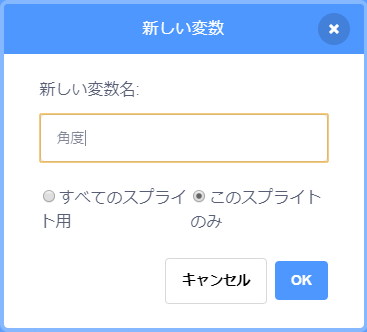
Sin 関数に渡す値を変え続けたいので、まずは変数が必要ですね。変数名は何でも良いですが、今回は"角度"と命名しました。日本語が嫌なら"Degree"とでも付けてあげると良いでしょう!
変数は、"このスプライトのみ"でオッケーです。
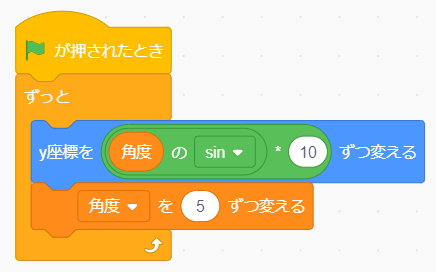
次に、上記のようなコードを組み込んでみましょう。
Sin 関数の結果は『-1.0 ~ 1.0』と小さい値なので、任意の数値を掛けて大きな振れ幅にしてあげます。角度を少しずつ変えて、サインカーブの値が返ってくるようにしたコードです。
動画のようになっていれば、正しくコードが組めています!
Sin 関数で曲線運動するネコ
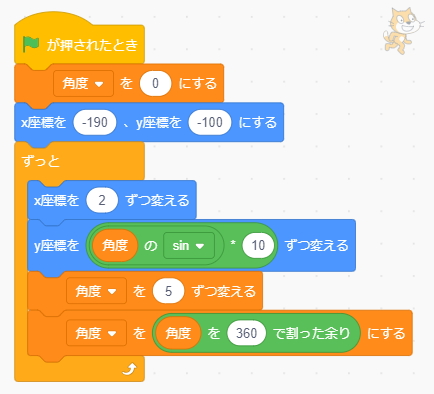
コードをいくつか追加しました!
- 角度変数の初期化
- X座標とY座標の初期化
- X座標を2ずつ変える
- 角度が『0~359』の範囲になる計算
Y座標が上下運動する移動に、X座標の移動が追加されて、波のような移動ができるようになりました!
動画のようになっていれば、正しくコードが組めています!
同じようにならない場合は、コードの間違いを探してみましょう。
Sin(サイン)とは
ここからは、ちょっとだけ Sin の仕組みを解説します。
中学・高校で『三角関数』を学習します。『Sin(サイン)』は三角関数の一つで、正式名称は Sine と表記します。
Sin はゲーム制作においても、使う回数がとっても多い手段です。Sin はプログラム界で『Sin 関数』と呼びます。Scratch でも Sin 関数が使えますね!
三角関数は理屈も大事なのですが、Sin 関数を扱えることはもっと大事です。理屈は抜きにして Sin 関数の仕組みを学んで、表現の幅を広げちゃいましょう!
サインカーブ
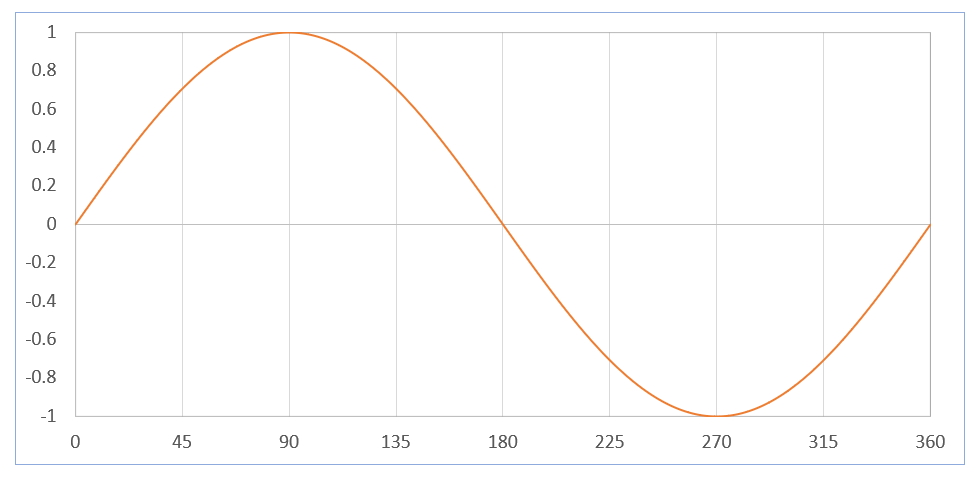
三角関数の理屈はナシといいましたが、このサインカーブの形だけを覚えておくと、Sin 関数を使うときにとっても役に立ちます!サインカーブのポイントをいくつかあげます。
- 横軸は『0』から始まって『360』で一周する
- 縦軸は『0』から始まって『0』で一周する
- 縦軸は『1.0』が最高値で、『-1.0』が最低値
- 『0 → 0.0』『90 → 1.0』『180 → 0.0』『270 → -1.0』
Sin 関数使うと、このサインカーブのような曲線状の値が得られると覚えておきましょう。
ディグリー法とラジアン法
ディグリー法やラジアン法に関しては、Scratch では特に気にしなくてもよい項目なのですが、本物のプログラミングでは覚えておかなければ少し困る内容なので、簡単に解説します。
ディグリー法
小学校で『分度器』を用いて、とある図形の辺Aと辺Bの角度を調べる授業があります。もし直角なら90°ですし、鋭角であるほど小さい角度になりますね。これが『ディグリー(Degree)法』です。
また、円は一周で 360°だと習うと思います。これは、サインカーブが 360 で一周する理由だったりします。
Scratch の Sin 関数で、0 や 90 や 180 などの数値を渡しましたが、つまりディグリー角を Sin 関数に渡していたことになりますね!
ラジアン法
『ラジアン(Radian)法』は、半径が1の円周の長さを表す方法です。
ちなみに、『円周率(π)』は、円の直径に対する円周の長さの比率のことで、直径が1の円のとき、3.141592…という値になります。
つまり、ラジアンは『半径 * 2 * 円周率』で表すことができるので、『0.0 ~ 6.283184…』という範囲になります。
ディグリー法・ラジアン法ともに共通していることは、どちらも円1周に対して何パーセントの割合を占めるかを表現していることです。
ディグリーとラジアンの変換
Scratch では、誰もがわかりやすいディグリー法で Sin 関数が利用できるようになっていますが、実際のプログラミングでは一般的にラジアン法が用いられます。
ラジアン値 = ディグリー値 / 180 * 円周率(3.141592…)
ディグリー値 = ラジアン値 * 180 / 円周率(3.141592…)
今後、プログラミングを学習していて Sin 関数にディグリー角を渡しても、結果がおかしいな?と思ったら、ラジアン法のことを思い出してあげてください!
おまけ
Sin 関数を応用して、シューティングゲームのような弾道を作ってみました。曲線移動ならでは動きでかっこよくないですか?
もしご要望があれば、おまけ動画の解説もしようかなと思っています!
以上、『Scratch』で『Sin関数』と『曲線運動』を学ぼうでした!